En 2022, cuando los países aún estaban lidiando con los efectos persistentes de la pandemia del COVID19, 30 800 estudiantes españoles de un total de 480 900 matriculados en el sistema educativo realizaban la evaluación internacional de la OCDE. El objetivo del Programa para la Evaluación Internacional de Alumnos de la OCDE (PISA) es medir la capacidad del alumnado de 15 años, que haya completado al menos seis años de educación formal, para utilizar sus conocimientos y habilidades de lectura, matemáticas y ciencias para afrontar los retos de la vida cotidiana.
Ser competente en matemáticas no es únicamente ser capaz de reproducir procedimientos matemáticos rutinarios. El marco teórico de PISA considera que una persona competente en matemáticas es alguien que puede razonar matemáticamente, es decir, que piensa matemáticamente de forma que puede resolver problemas complejos de la vida real, mediante la formulación, el empleo y la interpretación de las matemáticas.
Los últimos resultados de PISA2022 indican que el alumnado de Singapur obtuvo una puntuación significativamente superior a la de todos los demás países/economías en matemáticas (575 puntos), mientras que España, con 473 puntos de media, se encuentra solo a un punto por encima de los resultados de la OCDE. Las Comunidades Autónomas que se localizan por encima de la latitud 40oN (el paralelo de Castelló de la Plana), tienen resultados que oscilan entre 482 y 499 puntos con la salvedad de Cataluña. Por el contrario, en latitudes menores los valores varían entre 395 y 473 puntos. Estas cifras reflejan grandes desigualdades en la competencia matemática del alumnado español dependiendo de su ubicación geográfica, pues las diferencias llegan a los 104 puntos. Más allá de las diferencias numéricas de más de 100 puntos de media con el alumnado de Singapur o entre las diferentes Comunidades Autónomas, la interpretación de estos datos plantea dos interrogantes: ¿a qué es capaz de enfrentarse el alumnado de forma autónoma? y, ¿cuáles son las fuentes de inequidad en nuestro sistema educativo? Dar respuesta a estos interrogantes permitirá tomar decisiones coherentes para mejorar nuestro currículo y nuestro sistema educativo en general.
En esta entrada del Boletín de la RSME pretendemos dar respuesta a la primera cuestión, para lo que haremos un análisis minucioso del diseño de la prueba y de los resultados obtenidos.
El diseño de las pruebas PISA basa la estimación de la competencia del alumnado en los tipos de tareas que se espera que realicen con éxito. Esto significa que es probable que sean capaces de responder correctamente preguntas situadas en el nivel de dificultad asociado a su propia posición en la escala o por debajo del mismo. Por el contrario, es poco probable que puedan resolver con éxito cuestiones situadas por encima del nivel de dificultad asociado a su posición en la escala. Así, las escalas PISA para medir la competencia matemática se dividen en ocho niveles de rendimiento que corresponden a una horquilla de unos 62 puntos: 1c, 1b, 1a, 2, 3, 4, 5 y 6.
En el nivel 1c (valor inferior de esta categoría), el alumnado puede responder a preguntas sobre contextos de fácil comprensión en los que toda la información relevante se ofrece de forma clara, en un formato sencillo y familiar y se define en un texto muy breve y sintácticamente sencillo. Es capaz de seguir unas instrucciones claras que describen un único paso u operación.
La OCDE interpreta que los países con poco alumnado en los niveles 1a, 1b y 1c alcanzan este nivel básico de competencia matemática. Es el caso de países como Estonia, China Taipei, Hong Kong, Macao o Singapur, que tienen un 15 % de su alumnado en estos niveles. Sin embargo, en España este porcentaje es del 30 %. Además, el 10 % del alumnado español está en los niveles 1b y 1c, lo que significa que es incapaz de dar respuesta a una tarea como la mostrada en la Figura 1 (categorizada en el nivel 1a).
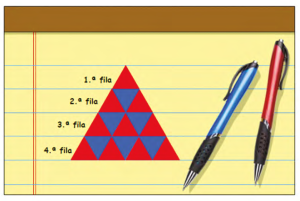
(Figura 1. Unidad CMA150. Figura con un patrón de triángulos. Anexo. Ejemplos de preguntas de matemáticas Estudio PISA 2022)
Aproximadamente el 28 % del alumnado español alcanza el nivel 2. Este alumnado es capaz de reconocer situaciones en las que se necesita diseñar estrategias simples para resolver problemas, incluyendo la realización de simulaciones sencillas en las que interviene una variable como parte de su estrategia de solución. Este nivel de competencia implica ser capaz de extraer información relevante de una o varias fuentes que utilicen modos de representación ligeramente más complejos -tablas bidireccionales, gráficos o representaciones bidimensionales de objetos tridimensionales-, así como demostrar una comprensión básica de las relaciones funcionales resolviendo problemas en los que intervienen proporciones sencillas e interpretando literalmente los resultados.
Otro 24 % del alumnado se encuentra en el nivel 3, donde se sitúa la media española solo un punto por encima de la media de la OECD. El alumnado que alcanza este nivel puede idear estrategias de solución, incluidas estrategias que requieren una toma de decisiones o flexibilidad en la comprensión de conceptos básicos. Además, es capaz de utilizar habilidades de pensamiento computacional para desarrollar su estrategia de solución y de resolver tareas que requieren la realización de varios cálculos diferentes, pero rutinarios, que no están claramente definidos en el enunciado del problema. Puede utilizar la visualización espacial como parte de una estrategia de solución o determinar cómo utilizar una simulación para recopilar datos apropiados de la tarea. Puede interpretar y utilizar representaciones en distintas fuentes de información y razonar directamente a partir de ellas, incluida la toma de decisiones condicionales utilizando una tabla de dos direcciones.
Aproximadamente un 12 % del alumnado español se encuentra en el nivel 4. Puede trabajar eficazmente con modelos explícitos para situaciones concretas complejas, en las que a veces intervienen dos variables, así como demostrar su capacidad para trabajar con modelos indefinidos que obtienen utilizando un enfoque de pensamiento computacional más sofisticado. En este nivel empiezan a abordar aspectos del pensamiento crítico, como la evaluación de la razonabilidad de un resultado mediante juicios cualitativos cuando no es posible realizar cálculos a partir de la información proporcionada. Puede seleccionar e integrar distintas representaciones de la información, incluidas las simbólicas o gráficas, relacionándolas directamente con aspectos de situaciones del mundo real. Puede construir y comunicar explicaciones y argumentos basados en sus interpretaciones, razonamientos y metodología.
El nivel 5 –en el que se encuentra la media de los estudiantes de Singapur– solo lo alcanza el 4 % del alumnado español. Este alumnado demuestra una mayor flexibilidad de formulación de estrategias. Puede desarrollar y trabajar con modelos para situaciones complejas, identificando o imponiendo restricciones y especificando supuestos. Puede aplicar estrategias de resolución de problemas sistemáticas y bien planificadas para abordar tareas más complejas, como decidir cómo desarrollar un experimento, diseñar un procedimiento óptimo o trabajar con visualizaciones más complejas que no se dan en la tarea. Demuestra una mayor capacidad para resolver problemas cuyas soluciones requieren a menudo la incorporación de conocimientos matemáticos que no se indican explícitamente en la tarea. Reflexiona sobre su trabajo y considera los resultados matemáticos en relación con el contexto del mundo real.
Finalmente, en el nivel 6 el alumnado es capaz de trabajar con problemas abstractos y demostrar creatividad y flexibilidad de pensamiento para desarrollar soluciones. Sabe relacionar distintas fuentes de información y representaciones, incluido el uso eficaz de simulaciones u hojas de cálculo como parte de la solución. Tiene un pensamiento crítico y domina los conceptos matemáticos simbólicos y formales que utiliza para comunicar con claridad sus razonamientos. Puede reflexionar sobre la idoneidad de sus acciones con respecto a su solución y a su situación original. Un ejemplo de pregunta que evalúa este nivel es:
En el siguiente gráfico se muestra el número total de DVD vendidos cada año en Reino Unido desde 2008 hasta 2014.
Los valores situados en el eje horizontal representan el número de años transcurridos desde 2008. Sitúa el cursor encima de los del gráfico para ver las coordenadas de cada punto. Por ejemplo, el punto (0; 252,9) indica que en 2008 se vendieron 252,9 millones de DVD. El punto (1; 234,6) indica que se vendieron 234,6 millones de DVD durante el año 2009, etc.
Se ha añadido una línea en el gráfico para modelizar estos puntos de datos.
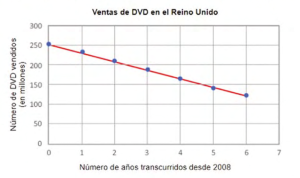
La ecuación de la línea es , donde es el número de DVD vendidos (en millones) y es el número de años transcurridos desde 2008.
Si esta tendencia en las ventas continúa, ¿en qué año el número de DVD vendidos será inferior a 1 millón según este modelo?
(Figura 2. Unidad CMA106Q02. Ventas de DVD. Anexo. Ejemplos de preguntas de matemáticas Estudio PISA 2022)
España, con solo un 6 % en los niveles 5 y 6, se encuentra en clara desigualdad con los 16 países/economías que presentan un 10 % del alumnado en dichos niveles. Entre ellos destaca Singapur, con aproximadamente un 45 % del alumnado en estos niveles de alto rendimiento. En la próxima entrada se discutirán las posibles causas de estos resultados y se esbozarán algunas medidas que podrían contribuir a mejorarlos en el futuro.




