Para la sección de la Comisión de Educación en el Boletín de esta semana, contamos con la colaboración de Gregorio Morales, profesor del IES Marjana en Chiva (Valencia). Con una sólida trayectoria en la implementación de las Thinking Classrooms en los primeros cursos de la Educación Secundaria Obligatoria, Gregorio es la persona ideal para compartir, de primera mano y en primera persona, cómo llevar a cabo este innovador enfoque en el aula.
Podríamos decir que la Thinking Classroom es la metodología de moda, y es probable que quienes lean esta entrada del Boletín semanal de RSME la conozcan. Pero, por si acaso, haré un breve resumen para explicar en qué consiste, cómo la he implementado en mi aula de 1º de ESO y por qué creo que entronca a la perfección con el currículum de la actual Ley de Educación.
En su libro Building Thinking Classrooms in Mathematics, Peter Liljedahl desarrolla esta metodología y, a través de sus 14 capítulos, muestra en qué consiste y cómo implementarla en el aula. Cada capítulo se centra en un aspecto clave, desde la configuración de los grupos de trabajo hasta la evaluación y calificación, pasando por el uso del cuaderno. No obstante, en lo que sigue me centraré en cuatro características básicas que, a mi juicio, definen una Thinking Classroom y que persiguen una cultura de aula orientada a la resolución de problemas:
Trabajo en equipo: cada sesión se conforma un nuevo equipo de 3 personas de manera totalmente aleatoria.
- Pizarras verticales borrables: los equipos están de pie, haciendo una piña contra el problema. Al ser superficies borrables, se fomenta la experimentación, la interacción, la búsqueda de estrategias y el aprovechamiento del error. Si la clase es suficientemente diáfana, se promoverá también el intercambio de ideas entre diferentes equipos.
- Problemas ricos: se plantean problemas ricos de suelo bajo (de fácil acceso para todos) y techo alto (con extensiones para que el problema no se acabe, y nunca deje de ser un reto para todos). Además, son problemas con múltiples estrategias para abordarlo que fomentan la negociación, la argumentación y el intercambio de ideas.
- Evaluación formativa y gestión de las preguntas: la evaluación formativa y el día a día de la clase aparecen unidas mediante el diálogo estudiante-estudiante y estudiante-docente. Es en estas interacciones donde se dan pistas, se proponen extensiones, y se comprueba no solo que se llega a un resultado correcto sino el procedimiento seguido, la justificación, la reflexión de los obstáculos encontrados, etc.
Yo empecé a utilizar esta metodología en 1º ESO del IES Marjana de Chiva (Valencia) en el curso 2022- 23, aplicándola en todas las sesiones de la asignatura (4h semanales) en un aula específica que montamos para este fin.

Colocamos 10 pizarras blancas de 90 cm x 120 cm y eliminamos la mesa del profesor y los pupitres, sustituyéndolas por mesas grandes. De este modo, alrededor de las paredes queda un espacio de casi 2 m que permite el flujo del docente y de los propios estudiantes por las pizarras.
Los problemas que proponemos siguen una secuencia de aprendizaje a través de la resolución de problemas. Es decir:
- Se plantean situaciones problemáticas sin que los alumnos reciban instrucción previa.
- Los problemas fomentan la negociación y la búsqueda de estrategias. Y mediante la resolución de estos problemas se descubren nuevos saberes.
- El docente usa estos descubrimientos (normalmente hago fotos de las pizarras) para hacer una consolidación e institucionalización de las nuevas estrategias y los nuevos saberes descubiertos.
- Se plantean nuevos problemas en los que habrá que poner en práctica estos nuevos saberes.
En cada sesión de estas secuencias los grupos se rehacen de manera aleatoria. De esta forma, los descubrimientos, las maneras de representar la información y las diferentes estrategias se van transmitiendo de unos a otros (cuando tres personas que ayer estaban en equipos distintos y, posiblemente, resolvieron el problema de ayer de tres modos distintos tendrán que negociar, comunicar y argumentar sus ideas para abordar el problema de hoy). Al cabo de cuatro o cinco sesiones, se ha construido un conocimiento colectivo alrededor de los problemas propuestos y llega el momento de la institucionalización.
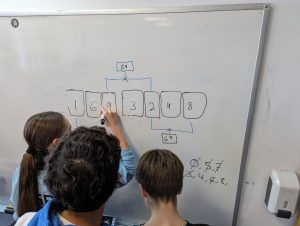
En la siguiente figura aparece un equipo que está en las primeras fases de investigación de este problema:
Encontrad un número de 7 cifras, todas distintas, en el que coincidan el producto de sus tres primeras, el producto de las tres cifras del medio y el producto de sus tres últimas cifras.
Este enfoque se alinea perfectamente con absolutamente todos los procesos matemáticos (NCTM, 2010) y competencias matemáticas (Niss, 2003) que en el currículum de la LOMLOE se han llamado competencias específicas. Se trabaja continuamente la resolución de problemas, la modelización, el hacer conjeturas (validarlas o refutarlas), la comunicación y la representación y el sentido socioafectivo (la gestión de las emociones tanto individual, en equipo y en gran grupo). Hay oportunidades para evaluar y mejorar todas estas competencias en todas y cada una de las sesiones.
Con esta metodología y con secuencias de problemas bien planteados y que despierten la curiosidad, se consigue que los alumnos disfruten desarrollando su capacidad de pensamiento matemático.
Para concluir esta entrada, queremos agradecer a Gregorio que nos haya regalado esta descripción de su experiencia justo ahora que vamos a poder disfrutar de la edición en español del libro de Peter Liljedahl.
Referencias
-Liljedahl, P. (2020). Building thinking classrooms in mathematics (Grades K-12): 14 Teaching practices for enhancing learning. Corwin Press Inc.
-NCTM (2010). Common Core State Standards for Mathematics. NCTM.
-Niss, M. (2003). Mathematical competencies and the learning of mathematics: The Danish KOM project. In A. Gagatsis, & S. Papastavridis (Eds.) , 3rd Mediterranean conference on mathematical education (pp. 115–124). Athens: Hellenic Mathematical Society and Cyprus Mathematical Society.




